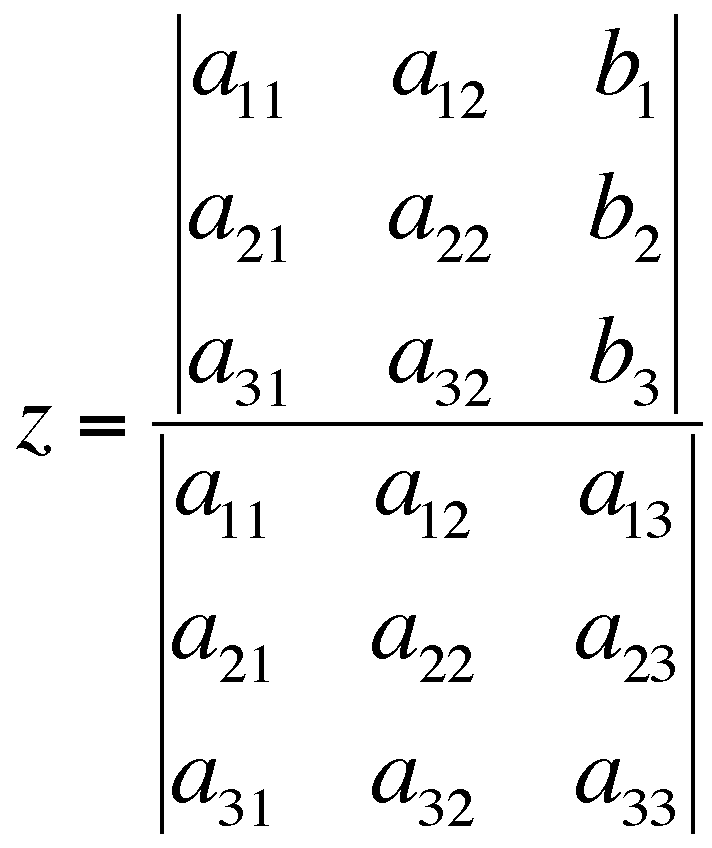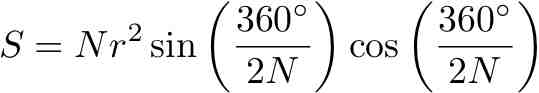課題７

以下の課題に関するレポートを、buturi-johoshori@tiger.kobe-u.ac.jp までメールで送りなさい

メールのsubjectは、report7 とし
レポートの一番最初に、氏名、学籍番号を記すこと
送付するのは、ソースコードのみ（実行ファイルは不要）

７−A：
次の２つの行列A, Bの交換関係 AB - BAを求めよ。
matrix A

matrix A

,

matrix B

　計算結果を見やすく出力するため行列c[3][3]を以下の様に出力しよう
       printf("matrix c= ¥n");
        for (i=0; i<SIZE; i++){
            for (j=0; j<SIZE; j++){
                printf("%d¥t",c[i][j]);
            }
        printf("¥n");
       }

　行列の積については、線形代数の教科書を参考にすること

７−B：
　３変数の連立１次方程式を解くプログラムを作ろう。
連立１次方程式の解はクラメルの公式として知られている。
３個の変数 x, y, z があるときに次のような係数をもつ連立１次方程式があるとする
          equetion

equetion

このとき、解 x, y, zは行列式をもちいて以下の通りとなる。
sol_x

sol_x

,

sol_y

,

sol_z

これを用いて、3つの連立１次方程式の係数９つを入力すると x, y, z を求めるプログラムを作ろう
プログラムの動作のチェックとして
        x + 2y - z = 2
        2x + y - z = 0
        3x - y + 2z = 10
の解は x=1, y=3, z=5 を用いよ。

７−C：
　内接多角形で円周率πを近似することを考える。図のように半径1の円の面積はS=π*1*1 =π 〜3.1415927...　である。

inner circle

この円に内接する多角形を考える。N角形は頂点の角度が360°/NであるN個の二等辺三角形に分割することができる。
すなわち、半径rの円に内接するN角形の面積は
area of poligon

area of poligon

となる。まず、N角形の面積を求めるプログラムを作り、次の問いに答えよ。
但し、sin(360°/N)関数とcos(360°/N)関数を含むプログラムであること。

（１）　このN角形の面積がπ〜3.0 で近似されるのは何角形のときか？
（２）　π〜3.14 で近似されるのは何角形のときか？

注意：double sin(double theta)　であるが、theta の単位はラジアンである。

７−D：
（１）　math ライブラリの中にある関数のうち double 型の関数の一覧を作れ。

ヒント：

mathライブラリーは、ヘッダーファイルmath.hに宣言が書かれている。ここから一覧を作るとよい。
math.hの置いてある場所は /usr/include の下である。/usr/include/math.hを見ると#if define行でマシンの
アーキテクチャによって/usr/include/architecture/ppc/math.hを読み込むようになっている。
（一般的にある特定のファイルを検索するにはMacOSX付属のファイル検索（アップルキー＋ f ）か、
ターミナル上で
            find / -name math.h -print
とすると、全ファイル検索をしてくれる。ただし、permission が許容されていないディレクトリは検索
できない。
math.h ファイル上では、関数として定義されている形式は
　      extern double cos( double );
などである。math.h ファイル上の"extern double"を含む行を抜き書きすればよい。これを行うには
grep が便利である。
例）   grep 'extern double' /usr/include/architecture/ppc/math.h

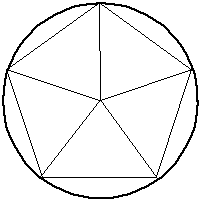
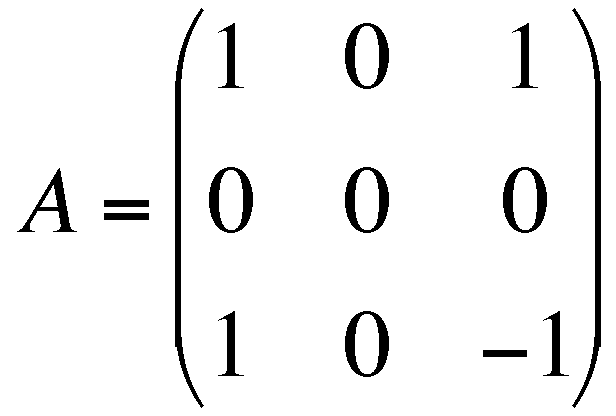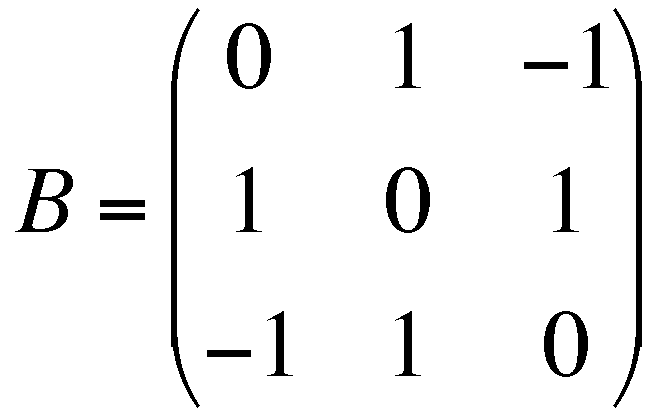
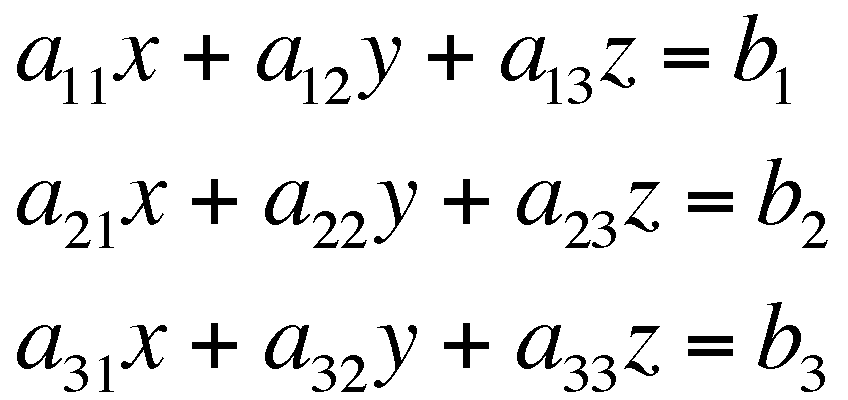
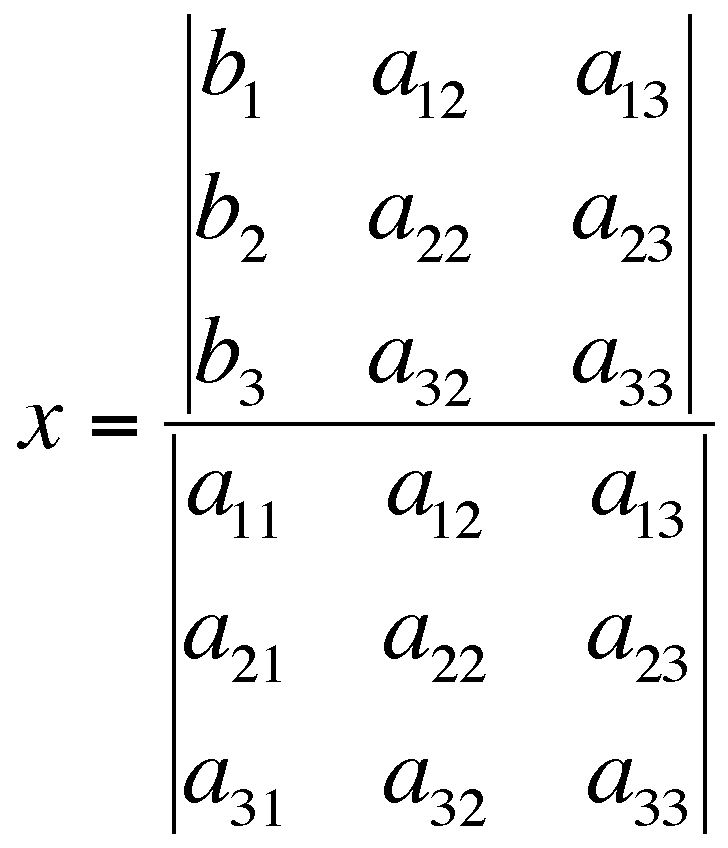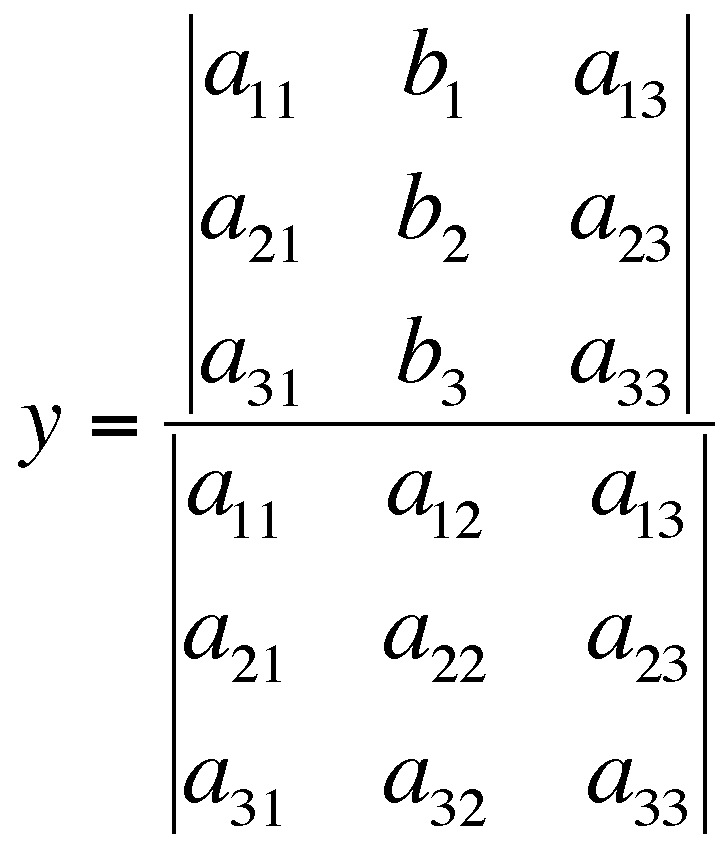（２）　math ライブラリの中にある floor, round の２つの関数は何をする関数であるか調べなさい

ヒント：

man -S 3 [関数名]　でマニュアルを見ることができる。